Nachfolgend finden Sie zwei mögliche Lösungen.
| Website: | Open E-Learning-Center Niedersachsen (OpenELEC) |
| Kurs: | Kompetenzen für das Unterrichten in der digitalen Welt |
| Buch: | Modul 05 |
| Gedruckt von: | Gast |
| Datum: | Montag, 23. Dezember 2024, 05:47 |
1.1 Was ist ein Algorithmus?
1.2 Algorithmus ja oder nein?
1.3 Implementieren von Algorithmen
Algorithmen sind zentraler Bestandteil der digitalen Welt. Was aber ist ein Algorithmus genau? Das erfahren Sie im untenstehenden Video.
Entscheiden Sie, ob folgende Handlungen durch einen Algorithmus beschrieben werden können!
Ein Algorithmus ist die konzeptionelle Lösungen für ein Problem. Zum Leben erweckt wird ein Algorithmus erst in einer Programmiersprache.
Die Umsetzung eines Algorithmus in eine Programmiersprache bezeichnet man als Implementierung.
Ein Programm implementiert also einen Algorithmus. Zusätzlich zu den Grundoperationen (in Snap! einzelne Blöcke) benötigen wir letztlich nur 3 sogenannte Strukturelemente: Sequenzen, Wiederholungen und Fallunterscheidungen.
Eine Folge von Anweisungen wird der Reihe nach ausgeführt.

Eine Folge von Anweisungen wird wiederholt.

Hier gibt es genau genommen (zwei) unterschiedliche Formen. Einmal eine Wiederholung mit fester Anzahl (im Beispiel 4; das kennen wir bereits) und einmal eine Wiederholung mit Bedingung (wiederhole solange bis du nicht mehr hungrig bist; das kennen wir noch nicht).

Es werden alternative Abläufe beschrieben. Falls wir hungrig sind, kochen wir etwas.

Um Fallunterscheidungen in unseren Algorithmen auch in Snap! umsetzen zu können, werden wir uns als Nächstes ansehen, was es mit den sechseckigen Blöcken auf sich hat und wie diese Fallunterscheidungen funktionieren!
2.1-2.2 Arten von Blöcken
2.3 Wahrheitswerte
2.4 Fallunterscheidung
2.5-2.10 Interaktives Malprogramm
2.12-2.14 Übungen zu Fallunterscheidungen
2.15 Komplexe Bedingungen
2.16-2.20 Exkurs: Spaß in Snap!
Wir haben bereits gesehen, dass es verschiedene Arten von Blöcken gibt. Um sie besser unterscheiden zu können, haben sie unterschiedliche Formen (und Namen):

Öffnen Sie die Vorlage. Führen Sie dann nacheinander die drei Blöcke unten im Bild aus!
Welchen Unterschied bemerken Sie?
Hinweis: Probieren Sie auch unterschiedliche Eingaben (z.B. 6 und 2 statt 2 und 5).

Der eckige (Befehls-)Block sage (Hallo!) "tut etwas": Er bringt das Objekt dazu etwas auf der Bühne zu "sagen".
Der zweite und dritte Block erzeugen Sprechblasen "direkt am Block", sie geben Werte zurück, haben aber keinen Effekt auf der Bühne.
Genau genommen gibt der zweite Block (Typ Funktion) einen beliebigen Wert zwischen 1 und 10 zurück, der dritte Block (Typ Prädikat) nur den Wert wahr oder falsch.
Einer Frage wie "Mauszeiger gedrückt?" oder Aussage wie "Heute regnet es" oder "1<3" lässt sich ein Wahrheitswert zuordnen. Es gibt nur zwei Werte, die ein Wahrheitswert annehmen kann: wahr und falsch (gewissermaßen ja und nein).
Blöcke, die Wahrheitswerte zurückgeben, haben wie gerade gesehen diese Form in Snap!:

Im Unterschied zu diesen Formen:
![]()
![]()
Entscheiden Sie, welchen Wahrheitswert die folgenden Blöcke zurückgeben!
Hinweis: Sie können die Blöcke hier in Snap! ausprobieren.
Solche Wahrheitswerte können wir dann nutzen, um in unserem Programm verschiedene Fälle zu unterscheiden.
Betrachten wir folgendes Beispiel:
Wir entwickeln ein Spiel und möchten Spielern die Möglichkeit geben, neue Gegenstände in einem Shop zu erwerben. Dafür benötigen sie Rubine. Klickt der Spieler nun auf die Schaltfläche "Kaufen", so muss zusätzlich geprüft werden, ob er über genügend Rubine verfügt, um den gewünschten Gegenstand überhaupt erwerben zu können.
Für solche Fälle bietet sich die Verwendung einer Fallunterscheidung an (im Englischen auch: if bzw. if-else statement (Anweisung)).
Eine Fallunterscheidung dient dazu, alternative Abläufe zu beschreiben.
Hinweis: Sie können deutsche Untertitel aktivieren.
In Snap! findet sich die Fallunterscheidung in der Kategorie Steuerung. Die Beispiele aus dem Video würden also sinngemäß zu:

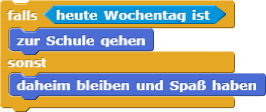
Hinweis: Sie sehen schon, Fallunterscheidungen gibt es in zwei Varianten, als einseitige (falls) und zweiseitige (falls-sonst) Fallunterscheidung.
Öffnen Sie dieses fast leere Snap!-Projekt und lassen Sie das Objekt dem Mauszeiger folgen!
Wenn (Grüne Flagge) angeklickt Block an. Klicken Sie dann die grüne Flagge rechts oben, um das Programm zu starten.
Eine mögliche Lösung finden Sie auf der nächsten Seite.
Mögliche Lösung zum Vergleichen (Schritt 1):

Nutzen Sie den Block "Stift runter" aus der Kategorie "Stift", um dem Objekt eine Malspur hinzuzufügen!
Tipp:
Mögliche Lösung zum Vergleichen (Schritt 2):

Nutzen Sie eine Fallunterscheidung und prüfen Sie, ob die Maustaste gedrückt ist! In diesem Fall soll der Block "Stift runter", in allen anderen Fällen der Block "Stift hoch" aufgerufen werden!
Tipps:
Objekte nicht mehr greifbar machen:
Sie greifen ein Objekt, wenn Sie dies mit der linken Maustaste anklicken und diese gedrückt halten. Es erscheint ein Schatten.
Für unser Malprogramm ist dieses Verhalten unpassend.
Entfernen Sie daher den Haken bei greifbar (unter dem Namen Ihres Objekts), damit das Objekt nicht mehr greifbar wird.


An zusätzlichen Blöcken benötigen wir noch:
![]()
![]()

Mögliche Lösung zum Vergleichen:

Hier eine Lösung, die auch Stiftfarbe und Stiftdicke ändert:

Hier eine Lösung, die zwei falls-Blöcke verwendet:

Hier noch eine weitere mögliche Lösung:
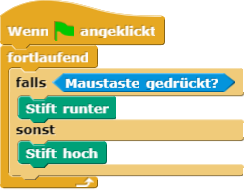
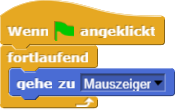
Wir können jeden Block, der einen Wahrheitswert zurückgibt, in der Bedingung eines falls- bzw. falls-sonst-Block verwenden.
Betrachten wir das folgende Skript, das Feedback zu einer erzielten Note gibt:

Wir haben verschiedene Fälle, die wir unterscheiden müssen. Das Skript prüft nacheinander alle bedingten Anweisungen. Trifft die zu prüfende Bedingung zu, werden die Blöcke im Inneren ausgeführt.
Öffnen Sie die Vorlage.
Stellen Sie eine Vermutung auf, was die Figur sagt, wenn Sie mit der Note 1, mit der Note 3 oder mit der Note 6 aufgerufen wird! Stimmt Ihre Vermutung mit dem eigentlichen Verhalten überein?
Mögliche Lösung zu Aufgabe 1 zum Vergleichen:
Bei Note 1 sagt die Figur "Sehr gut! Weiter so!", denn 1 ist kleiner als 3.
Bei Note 4 sagt die Figur "Nochmal gut gegangen!".
Bei Note 6 sagt die Figur "Das nächste mal wird's was!", da 6 größer ist als 4.
Erstellen Sie einen Skript, das das Kostüm des Zauberers abhängig vom Wetter (Regen oder Sonne) ändert!
Wenn es regnet, sollte der Zauberer einen Regenschirm beschwören, bei Sonne sollte er ihn verschwinden lassen.
Neben den Blöcken, mit denen Sie das Kostüm wechseln, die wir Ihnen bereits in den Skriptbereich gelegt haben, benötigen Sie Blöcke aus den Kategorien Operatoren, Variablen und Steuerung.

![]()
![]()
Mögliche Lösung zu Aufgabe 2 zum Vergleichen:


Einfache Bedingungen können wir nun ausdrücken. Allerdings benutzen wir im Sprachgebrauch oftmals komplexere Bedingungen:
Was wir dabei ganz instinktiv verwenden, können wir auch mit Blöcken ausdrücken:

Überlegen Sie, zu welchem Wahrheitswert die folgenden Blöcke ausgewertet werden!
Hinweis: Sie können die Blöcke hier in Snap! ausprobieren. Zerlegen Sie die Blöcke auch gern in ihre Einzelteile und führen Sie diese aus, um zu verstehen, was sie machen.
Das grundlegende Handwerkszeug für die Implementierung beliebiger Algorithmen in Snap! kennen Sie jetzt.
Falls Sie Lust haben unser Malprogramm von vorhin zu erweitern, haben wir Ihnen in diesem optionalen Exkurs ein paar Hilfestellungen zusammengestellt, um dem Programm einen kleinen Kniff zu verpassen.
Finden Sie diesen Bereich in Ihrem Snap!-Fenster (rechts, unter der Bühne).

Klicken Sie mit der rechten Maustaste auf das Objekt. Wählen Sie Duplizieren.

Mögliche Lösung zu Schritt 1:
Neben Ihrem bisherigen Objekt sollte ein neues Objekt mit dem Namen Objekt(2) entstanden sein.

Wir wollen nun erreichen, dass dieser Stift etwas anderes malt. Versichern Sie sich, dass Sie Objekt(2) ausgewählt haben (angedeutet durch den Rahmen) und tauschen Sie den Block gehe zu (Mauszeiger) durch die folgende Block-Kombination aus!
Hinweis: Sie werden noch keinen Unterschied sehen. Auch der Block gehe zu (Mauszeiger) stellt eine Abstraktion dar (eben genau von dieser Blockkombination).
gehe zu (Mauszeiger) und wählen Sie Löschen.

Ziehen Sie den Block gehe zu x: () y: () aus der Kategorie Bewegung an die Stelle.
Ziehen Sie dann die Blöcke Maus x-Position und Maus y-Position.

Mögliche Lösung von Schritt 2:
Bisher sollte das Skript so aussehen:
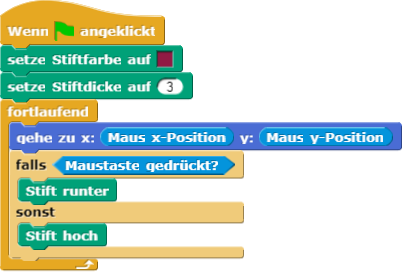
Bisher sehen wir noch keinen Effekt: Wir haben eine Implementierung durch eine andere ausgetauscht.
Ändern Sie die Stiftfarbe von Objekt(2)!
Tipp: Stiftfarbe verändern
Klicken Sie auf das farbige Quadrat im Block setze Stiftfarbe auf ☐.

Mögliche Lösung zu Schritt 3:

Hinweis: Sie sehen jetzt nur noch die blaue Linie, da der rote Stift vom blauen Stift übermalt wird.
Wie können wir nun dafür sorgen, dass Objekt(2) etwas anderes malt?
Eine Möglichkeit ist: Wir lassen Objekt(2) nach unten gehen, wenn die Maus nach oben geht.
Das können wir erreichen, indem wir die y-Koordinate umdrehen.
Invertieren Sie die y-Richtung, indem Sie die folgende Änderung vornehmen:
Ersetzen Sie den Block ![]() durch
durch ![]()

Mögliche Lösung zu Schritt 4:

Hier gibt's das komplette Projekt.
Hier ist noch längst nicht Schluss!
Momentan spiegelt unser Programm den Stift nach oben bzw. unten. Fügen Sie doch zwei weitere Objekte zum Projekt hinzu, die die Mausbewegung in weitere Richtungen (z.B. rechts bzw. links) spiegeln, um ein Kaleidoskop zu erzeugen!
-------------------------------------
Dieser Inhalt stellt ein Derivat des unter CC-BY-SA lizenzierten Inhalts Verkehrt herum gemalt - Spiegelbild von Jadga Hügle und Jens Mönig dar.
3.1-3.4 Eigene Blöcke erstellen
3.5-3.6 Exkurs: Funktionsblöcke
Im Video zu Algorithmen haben wir gelernt, dass Algorithmen selbst wieder Bausteine für Algorithmen sein können. Tatsächlich verfügt auch jeder der Blöcke in Snap! über einen Algorithmus, der ihm sagt, welche Schritte er befolgen muss um das zu tun, was er tut.
Wieder zeigt sich das Prinzip der Abstraktion mit: Wir müssen nicht alle Details eines Blocks verstehen, um ihn nutzen zu können. Und auch wir können komplexere Algorithmen in einen eigenen Block verpacken!
Um Algorithmen als Teil von Algorithmen in Snap! übersichtlich darstellen zu können, greifen wir häufig auf eigene Blöcke zurück. In diesem Abschnitt wollen wir uns ansehen, wie wir eigene Blöcke erstellen.
Werfen wir einen Blick auf noch einen anderen Algorithmus, den wir bereits in Modul 01 entworfen haben.
Ein Algorithmus, der ein Quadrat zeichnet.
Seine Implementierung sah so aus:
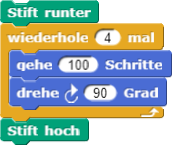

Wir werden diese Skripte nun in eigene Blöcke auslagern.
zeichne Polygon mit (seitenzahl) SeitenIm Modul 01 haben wir ein Skript erstellt, das ein beliebiges Polygon (n-Eck) zeichnet.
Öffnen Sie die Vorlage und erstellen Sie einen eigenen Block, der ein beliebiges Polygon (n-Eck) zeichnet. Der Block soll eine Eingabe seitenzahl für die Seitenzahl entgegennehmen.
Klicken dazu auf die Schaltfläche 'Neuer Block', die wir am Ende jeder Kategorie der Palette finden und erstellen einen neuen Befehlsblock.
Es öffnet sich ein neues Fenster, in dem Blöcke genau wie Skripte im Skriptbereich editiert werden können.

Bearbeiten....Achten Sie beim Erstellen des Blocks darauf, dass seitenzahl als Eingabe und nicht als Beschriftung ausgezeichnet ist.
Klicken Sie auf ein Wort wie seitenzahl um es von Beschriftung zu Eingabe zu ändern oder umgekehrt.

Mögliche Lösung:
Eine möglich Lösung ist:
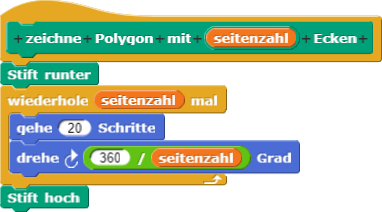
zeichne Polygon mit (seitenzahl) Ecken so, dass er auch eine Eingabe für die Seitenlänge entgegennimmt!Mögliche Lösung zum Vergleichen:

Weiter geht's:
Schreiben Sie ein Skript, in dem Ihr gerade erstellter Block mindestens 3 mal aufgerufen wird!
Mögliche Lösung zum Vergleichen:
Hier sind viele Lösungen denkbar. Sie können den Block in einer Sequenz mehrfach aufrufen:

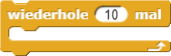
oder innerhalb einer Wiederholung verwenden:

In diesem optionalen Exkurs wollen wir uns ansehen, wie wir Blöcke dazu bringen können, Werte zurückzugeben.
Damit ein Block auch Werte zurückgeben kann, wird ein spezieller Block verwendet: berichte () aus der Kategorie Steuerung.
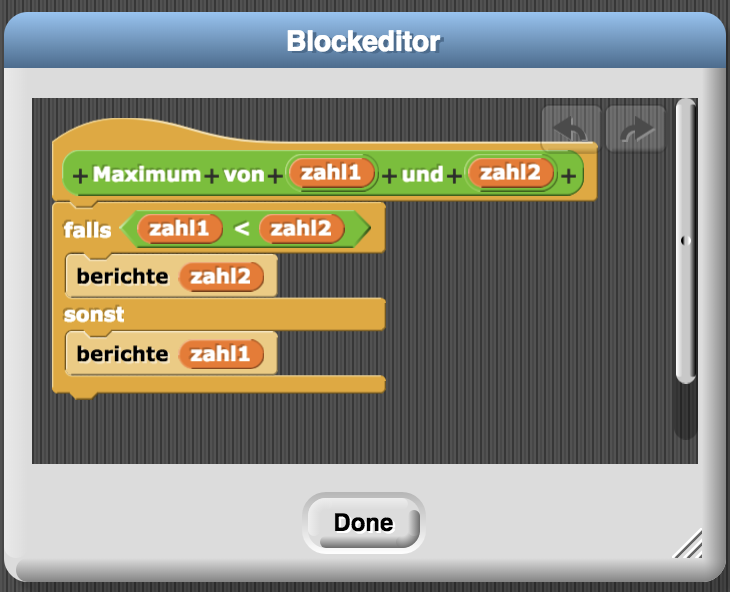
Nachdem Sie bereits wissen, wie Sie einen eigenen Befehlsblock erstellen, ist der Schritt zu einem eigenen Funktionsblock gar nicht weit. Die untenstehende Aufgabe führt Sie in die Erstellung eines eigenen Funktionsblocks ein, indem Sie einen bestehenden Block modifizieren dürfen. Sie können gerne die Tipps verwenden!
Öffnen Sie die Vorlage und betrachten Sie den Block "Maximum von zahl1 und zahl2".
Modifizieren Sie diesen so, dass er das Maximum von 3 Zahlen ermittelt!
Bearbeiten.... Erweitern Sie den Hutblock passend.
Die logischen Ausdrücke und, oder bzw. nicht könnten Ihnen helfen. Sie werden dann aber noch zusätzlich falls-Blöcke benötigen.

Es sind unterschiedliche Lösungen möglich.
Tipp: Weitere BlöckeSie werden nicht umhin kommen, zusätzliche Blöcke aus der Kategorie Steuerung zu verwenden. Versuchen Sie einen dieser Blöcke:


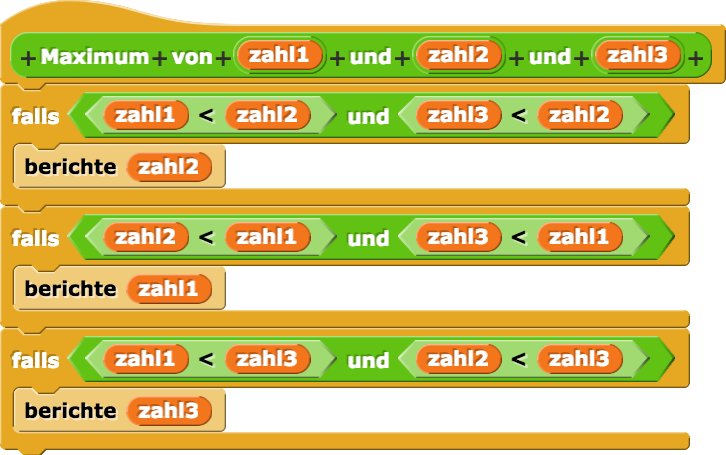
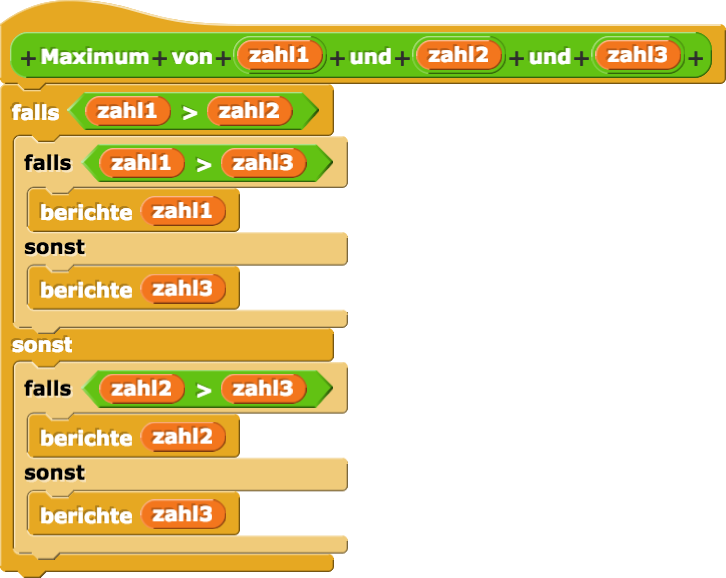
Nachfolgend finden Sie zwei mögliche Lösungen.


4.1 Algorithmen und Gesellschaft
4.2 Exkurs: Algorithmen in der Grundschule
"Algorithmen" sind nicht nur wichtiger, für sich stehender Bestandteil der KMK-Kompetenzen. Sie spielen auch in den unterschiedlichsten Disziplinen eine Rolle, entscheiden doch Algorithmen, welche Suchergebnisse wir erhalten, welche Nachrichten wir lesen oder welche Produkte uns angezeigt werden. Auch die Überwachung dutzender Server oder die Auswertung seismographischer Daten erfolgt durch Algorithmen. Schreiben wir Texte digital, so unterstützt uns die Rechtschreibkorrektur – noch etwas hinter dem Algorithmen stecken.
Algorithmen beeinflussen unser Handeln und treffen zudem Entscheidungen, die uns auch persönlich betreffen. Wir haben Ihnen im Folgenden einige Beispiele herausgesucht.

Bei der Routenplanung ist es die Aufgabe der Algorithmen den schnellsten, kürzesten, wirtschaftlichsten oder landschaftlich schönsten Weg von einem Start- zu einem Zielort zu finden. Algorithmen werden hier eingesetzt, um uns das Leben angenehmer zu machen. Ein bekannter Algorithmus, der genau diesen Weg findet, ist übrigens der Dijkstra-Algorithmus.
Auch wenn manch einer sich so sehr auf sein Navigationssystem verlässt , dass er schonmal stundenlang in die falsche Richtung fährt oder ins Meer stürzt, weil die noch in Bau befindliche Brücke auf seinem Navigationssystem schon existiert, würden wir Navigationssysteme vermutlich als unproblematisch beschreiben.
Nachdem Computer deutlich schneller rechnen können als wir Menschen, ist ihr Einsatz im Börsenhandel nicht abwegig. Wie groß der Anteil der Computer-Broker wirklich ist, überrascht viele: Bereits 2012 wurden 85 Prozent des US-Aktienhandels von Algorithmen durchgeführt.
Dahinter verbergen sich komplexe mathematische Formeln, die versuchen aus historischen Marktdaten und aktuellen Marktsignalen Rückschlüsse auf den besten Zeitpunkt für An- bzw. Verkauf zu schließen. Das das nicht immer reibungslos klappen muss, zeigte sich am Schwarzen Montag 1987, dem ersten Börsenkrach nach dem zweiten Weltkrieg.
Filterblasen sind ein Phänomen, das vor allem im Kontext sozialer Netzwerke und Suchmaschinen existiert. In der Kategorie #kurzerklärt beschreibt die Tagesschau, was unter Filterblasen zu verstehen ist.
Personalabteilungen nutzen Algorithmen, um die richtigen Bewerber für das eigene Unternehmen auszuwählen. Aus Modul 00 wissen wir, dass in Zukunft Kompetenzen in den Bereichen Kreativitität, kritisches Denken, Kollaboration und Kommunikation besonders wichtig sind. Festzustellen, ob ein Bewerber diese Kompetenzen mitbringt, ist nicht leicht und Entscheidungen basieren oft rein auf der eigenen Intuition. In Großbritannien und den USA werden daher über 70% der Bewerbungen zunächst von Algorithmen bewertet, ehe ein Mensch die Bewerbung sichtet.
Der Wunsch hinter dem Einsatz von Algorithmen ist, dass sie zuverlässiger und vor allem objektiver Entscheidungen treffen.
Berichte aus der Praxis zeigen, dass dem nicht immer so ist. Der folgende Tweet fasst das pointiert zusammen.

Die US-Justizbehörden nutzen Algorithmen, die abschätzen, ob eine Straftäterin bzw. ein Straftäter wieder rückfällig wird. Das hat direkte Auswirkungen auf alle Betroffenen, beeinflusst die Entscheidung doch ihr Strafmaß.
In den letzten 20 Jahren wurden solche Algorithmen bei mehr als einer Million Angeklagten eingesetzt. Die mit den Algorithmen verbundene Hoffnung waren fairere Entscheidungen (als sie Menschen treffen würden).
Obwohl der Algorithmus keine Information über die ethnische Herkunft der Angeklagten hatte, wurden schwarze bzw. weiße Angeklagte unterschiedlich behandelt. Der Algorithmus ist nicht nur nicht gut, wie Studien zeigen, sondern ist zudem auch nicht fair.
Übrigens: Für die letzten beiden Beispiele gilt: Hier werden häufig Algorithmen aus dem Bereich der Künstlichen Intelligenz verwendet. Wenn Sie mehr dazu erfahren wollen, finden Sie unter aiunplugged.org Anregungen, wie Sie künstliche Intelligenz anhand einfacher, spielerischer Aktivitäten nachvollziehen können. Die Beispiele sind übrigens auch für den Unterrichtseinsatz geeignet.
Hinter dem Einsatz von Algorithmen steht der Wunsch, Entscheidungen schneller, besser und objektiver zu treffen als Menschen.
Auch in der Grundschule lassen sich Algorithmen praktisch ausprobieren. In Ländern wie der Schweiz oder England ist Informatik und damit unter anderem das Thema Algorithmen übrigens bereits Stoff in der Grundschule.
CS Unplugged (Computer Science Unplugged, also Informatik ohne Strom) beschreibt einen Ansatz, Informatik ganz ohne Rechnereinsatz anfassbar zu machen. Informatische Konzepte wie Algorithmen werden spielerisch mit Karten, Schnüren oder durch Herumrennen im wahrsten Sinne des Wortes begreifbar.
Ein Beispiel zeigen die Entwickler von CS Unplugged in ihrem Video zu Sortieralgorithmen. Dort haben die Kinder unterschiedlich schwere Gewichte und eine Waage vor sich. Ihre Aufgabe ist es die Objekte möglichst schnell nach Gewicht zu ordnen. Dabei zeigt sich: Mit dem richtigen Algorithmus geht das vergleichsweise flott und es werden deutlich weniger Schritte benötigt.
Hinweis: Es gibt noch viele weitere Ideen zu CS Unplugged, auch zu anderen Themen als Algorithmik. Die Beispiele zeigen, dass auch zunächst "digitale Themen" von einer "ganz analogen" Vermittlung profitieren können.
Es gibt jede Menge kleiner Roboter, die programmierbar sind und sich in unterschiedlichen Altersstufen einsetzen lassen. Die von der Optik an eine Biene angelehnten BeeBots (siehe Video) lassen sich durch Tasten programmieren, eine Abfolge von Bewegungen durchzuführen. Der Ozobot fährt Linien ab und lässt sich mit Filzstift über Farbcodes (aber auch vom Computer aus) programmieren.
Hinweis: Wir stehen in keiner Weise in Verbindung mit den Herstellern dieser Produkte. Die Produkte dienen nur als Beispiele für Medien, die bereits jetzt in Grundschulen weltweit eingesetzt werden.
Scratch, das schweizer Taschenmesser unter den Informatikwerkzeugen an Grundschulen, wirkt auf den ersten Blick wie eine einfache Website zum Programmieren lernen. Aber Scratch ist viel mehr: Genau wie Snap! regt es dazu an Dinge auszuprobieren und selbst kreativ zu werden. Dabei gerät auch das eigentliche Programmieren schnell in den Hintergrund.
Anregungen finden Sie beispielsweise hier.

Wofür stellt dieser Block eine abgekürzte Schreibweise dar?

Option A

Option B
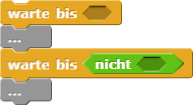
Option C

Option D