Modul 09
| Website: | Open E-Learning-Center Niedersachsen (OpenELEC) |
| Kurs: | Kompetenzen für das Unterrichten in der digitalen Welt |
| Buch: | Modul 09 |
| Gedruckt von: | Gast |
| Datum: | Montag, 23. Dezember 2024, 05:38 |
Inhaltsverzeichnis
- 1. Simulationen
- 2. Modellieren
- 3. Simulieren in fachlichen Kontexten
- 3.1. Makro- und Mikrosimulationen
- 3.2. Räuber-Beute-Simulation in Snap!
- 3.3. Räuber-Beute-Simulation in Snap! - Lösung I
- 3.4. Räuber-Beute-Simulation in Snap! - Mehr Hasen
- 3.5. Räuber-Beute-Simulation in Snap! - Lösung II
- 3.6. Räuber-Beute-Simulation in Snap! - Geschwindigkeit der Luchse reduzieren
- 3.7. Räuber-Beute-Simulation in Snap! - Lösung III
- 3.8. Räuber-Beute-Simulation in Snap! - Erkenntnisse gewinnen
- 3.9. Simulation einer Pandemie
- 3.10. Simulation einer Pandemie - Lösung
- 4. Simulationen im Unterricht
- 5. Selbsttest
- 6. Abschluss Modul 09
- 7. Literaturempfehlungen Modul 09
1. Simulationen
Überblick über die Kapitel:
Mit Simulation Fragen beantworten
1.1. Mit Simulation Fragen beantworten
Unten finden Sie eine Verkehrssimulation, in der 8 verschiedene Szenarien simuliert werden können.
Probieren Sie es aus und beantworten Sie damit unsere Frage!
Hinweis: Gerne dürfen Sie auch selbst Hypothesen aufstellen und versuchen diese mithilfe der Simulation zu beantworten.
Hinweis Szenario 1-4
Das 8 Szenario fehlt in der Abbildung noch, ist aber für die Aufgabe nicht relevant.
Der Infobutton innerhalb der Simulation liefert interessante Hinweise und Erklärungen.
Hinweis: Ändern Sie den Parameter LKW-Anteil unter Verkehrsflüsse und Allgemeines.
1.2. Modelle und Simulationen
Ein Modell ist eine Computerdarstellung eines Objekts (oder Systems von Objekten). Das kann zum Beispiel das Modell einer Autobahn sein.
Eine Simulation ist ein Algorithmus, der ein Modell nutzt, um zu sehen, was unter bestimmten Bedingungen im Laufe der Zeit geschehen wird. Wenn wir das Modell einer Autobahn nehmen, können wir beispielsweise simulieren, was passiert, wenn wir Tempolimits einführen.
Simulationen dienen der Analyse vor allem von dynamischen Systemen. Simulationen sind beispielsweise dann das Mittel der Wahl, wenn ein anderes (bspw. experimentelles) Vorgehen ...
...zu teuer wäre.
Autohersteller simulieren das Unfallverhalten ihrer Autos, ehe sie echte Autos im Crashtest untersuchen. Das spart Kosten, denn unzählige Testfahrzeuge in echten Crashtests zu untersuchen bis die perfekte Bauweise gefunden ist, wird sehr teuer.... zu zeitaufwändig wäre.
Testen, wie sich der Klimawandel auswirkt, würde Jahrzehnte wenn nicht gar Jahrhunderte dauern (auf jeden Fall wäre es dann auch zu spät etwas zu ändern).... zu gefährlich wäre.
Herausfinden, ob ein Atomkraftwerk einen Flugzeugabsturz übersteht, sollte man auch besser mit einer Simulation.... aus ethischen Gründen nicht vertretbar ist.
Besser wir simulieren, wie schnell sich COVID-19 verbreitet, als dass wir es ausprobieren.Die Daten bzw. Erkenntnisse, die eine Simulation liefert, können dann als Entscheidungshilfen herangezogen werden. Manchmal entstehen so auch neue Hypothesen, die dann durch eine Analyse vorhandener Daten bekräftigt werden können.
2. Modellieren
Überblick über die Kapitel:
Modellieren I
Modellieren II
Concept Maps
2.1. Modellieren I
Jede Simulation benötigt ein zugrundeliegendes Modell. In diesem Abschnitt wollen wir die wesentlichen Eigenschaften eines Modells herausarbeiten. Dazu wollen wir uns auf ein sehr bekanntes Modell konzentrieren.
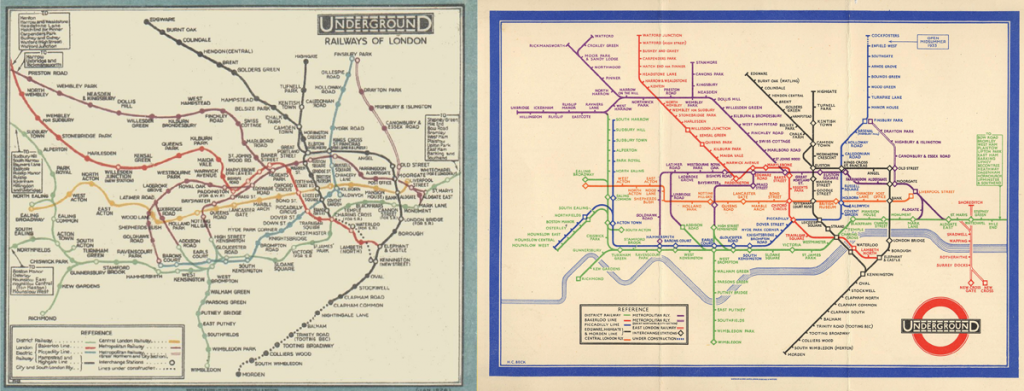
Die Stadt London ist bekannt für den Big Ben, die Tower Bridge und ein Stück weit auch für ihre U-Bahn – insbesondere für ihren U-Bahn-Netzplan. Betrachten Sie die beiden Versionen des U-Bahn-Netzplans von London. Worin unterscheiden sie sich?
Lösungshinweise finden Sie auf der nächsten Seite.
2.2. Modellieren I - Lösungshinweise
Aus dem Netzplan von 1926 kann der Kurvenverlauf herausgelesen werden und auch die Distanzen sind erkennbar. Auf dem Netzplan von 1933 hingegen sind mehr Stationen abgebildet, da kein Wert auf reale Distanzen gelegt wurde. Lediglich die Themse bietet räumliche Orientierung. Aus heutiger Sicht würden wir diesen Netzplan gegenüber seinem Vorgänger als übersichtlicher beschreiben.
Tatsächlich aber wurde der Netzplan von 1933 zunächst abgelehnt. Für die Betrachter war nicht erkennbar, wie weit einzelne Stationen auseinanderliegen. Wie Sie aber wissen, ähnelt heute jeder U-Bahn-Netzplan dem, den ein Mann namens Harry Beck 1933 entwickelte. Im Gegensatz zu bisher üblichen Netzplänen fokussierte sich sein Netzplan darauf darzustellen, wie einzelne Stationen verbunden sind (Topologie), um eine schnelle Orientierung im U-Bahn-Netz zu ermöglichen, und nicht auf geographische Details. Und schon bald hatten auch die Bewohner Londons dies erkannt.
Hier greift wie bei der Umwandlung von analogen in digitale Werte das Prinzip der Abstraktion. Zur Erinnerung:
Abstraktion bedeutet irrelevante Details weglassen und dadurch Komplexität bewältigen. Ohne Abstraktion wären moderne digitale Systeme so nicht denkbar.
2.3. Modellieren II
Modelle helfen den Überblick über ansonsten unüberschaubare bzw. komplexe Strukturen zu gewinnen. Gegenüber dem Original ist es mittels Modellen leichter Informationen zu gewinnen, Erfahrungen zu sammeln, Schlussfolgerungen anzustellen, Alternativen zu bewerten oder Entscheidungen zu treffen. Auch Simulationen liegen bestimmte Modelle zugrunde, die versuchen das Systemverhalten möglichst realitätsgetreu zu beschreiben.
In Simulationen werden also genau genommen Modelle bzw. Modellparameter manipuliert und die Auswirkungen dieser Manipulationen beobachtet.
Wie uns Modellierung und Simulation bei der Orientierung in einer komplexer werdenden Welt helfen, erfahren Sie im Video.
Die Bedeutung des Modellierens
Im Buch Digitale Kompetenz führen Hartmann und Hundertpfund "die Fähigkeit, komplexe Sachverhalte und große Datenmengen in abstrakte Konzepte zu übersetzen sowie Modelle zu bilden und auszuwerten" als eine der 10 wichtigsten digitalen Kompetenzen auf. Darüberhinaus sind Modelle auch für das Lernen grundlegend: Lernende konstruieren sich ganz natürlich mentale Modelle von Phänomenen oder Prozessen in ihrer Umwelt, also gedanklichen Vorstellungen darüber, wie ein System funktioniert.
Die Interaktion mit (fertigen) Mikrowelten hat allerdings keine Auswirkungen auf die mentalen Modelle. Da die Realität häufig deutlich komplexer ist als wir dies in Modellen abbilden können, schließt das Modellieren unabhängig von zugrundegelegter Theorie bzw. zugrundegelegten Daten immer gewisse Abstraktionen und Verallgemeinerungen mit ein. Beim Modellieren müssen demnach bewusst Entscheidungen getroffen werden. Diese Entscheidungen sind auch entscheidend für den Lernfortschritt. Sollen mentale Modelle verbessert bzw. gelernt werden, sollte im Unterricht daher auch Wert auf die Modellierung gelegt werden (Jonassen, 2006).
2.4. Concept Maps
Nicht immer ist es jedoch (sinnvoll) möglich konkrete Modellierungen im Unterricht zu thematisieren. Bewährt hat sich daher wiederholt das Finden von Analogien oder das Suchen von Gemeinsamkeiten bzw. Mustern in verschiedenen Themen anzuregen.
Eine weitere Möglichkeit Abstraktion und Modellbildung zu üben, stellen sog. Concept Maps dar. Concept Maps können in allen Jahrgangsstufen dazu verwendet werden, Wissenstrukturen als grafische Netzwerke aus Konzepten (Knoten) und Beziehungen zwischen diesen (Kanten) darzustellen. Damit erinnern sie zunächst an Mindmaps. Allerdings gehen alle Gedanken in Mindmaps von einem zentralen Begriff aus. Bei Concept Maps hingegen sind die Beziehungen beschriftet und auch beliebige Querverbindungen möglich.
Mit Hilfe solcher "Karten" kann die semantische Struktur des angeeigneten Wissens oder eines zu erschließenden Textes kompakt dargestellt werden. Im Laufe des Schuljahrs können die Karten außerdem kontinuierlich erweitert werden. Durch die fortlaufende Erweiterung einer kompakten Darstellung des eigenen Wissens lassen sich Dinge besser merken als durch das Memorieren von Notizen bzw. Hefteinträgen. Auch Studien bestätigen den nachhaltigen Effekt für das Lernen (J. Nesbit, O. Adesope, 2006).

Obenstehende Abbildung zeigt eine Concept Map über Concept Maps. Dabei sind die in Boxen gesetzten Begriffe (etwa "Concept Maps", "Organized Knowledge" oder " Associated Feelings or Affect") Konzepte. Die an Pfeilen notierten Begriffe (etwa "represents", "includes", "necessary for") sind Beziehungen. Zwei Konzepte und eine Beziehung bilden zusammen eine Aussage: "Concept Maps represent Organized Knowledge", oder "Organized Knowledge needed to answer Focus Question(s)".
Resümieren Sie diesen Abschnitt, indem Sie Ihre persönliche Concept Map zum Themenbereich Modellieren erstellen. Zeichnen Sie Ihre Concept Map per Hand oder nutzen Sie ein Softwaretool zur Erstellung, etwa das webbasierte draw.io.
Vergleichen Sie Ihre Concept Map mit den Mitgliedern Ihrer Lerngruppe. Kommentieren Sie Ihren Beitrag: Würden Sie etwas an Ihrer Concept Map verändern?
Concept Maps untereinander vergleichen
Für das Lernen förderlich ist es, Concept Maps mit anderen zu vergleichen. Es eröffnet die Möglichkeit andere Darstellungen und Strukturierungen derselben Ideen und Konzepte zu erfahren und daraus zu lernen.
3. Simulieren in fachlichen Kontexten
Überblick über die Kapitel:
Makro- und Mikrosimulationen
Räuber-Beute-Simulation in Snap!
Simulation einer Pandemie
3.1. Makro- und Mikrosimulationen
Wie Simulationen funktionieren wollen wir uns nun an einem Beispiel ansehen.
Der kanadische Luchs ist zum Überleben auf Schneeschuhhasen angewiesen, stellen diese doch 35 bis 97% seiner Nahrung dar (Hunter, 2015).
Mithilfe unserer Simulation wollen wir die Räuber-Beute Beziehung zwischen Schneeschuhhasen und Luchsen in Kanada untersuchen. Entsprechend des Modellierungsgedankens fokussieren wir uns in unserem Modell auf die Beziehung "Luchse fressen Hasen" und vernachlässigen etwaige andere Einflüsse.
Makro- und Mikrosimulationen
Makrosimulation

Mikrosimulation

Makrosimulation
Bei einer Makrosimulation ist es unser Ziel, ein System zu simulieren, ohne die einzelnen Bestandteile in besonderer Weise zu betrachten. Ein solches Vorgehen würden wir beispielsweise zur Hochrechnung von Bevölkerungs- und Schülerzahlen oder für die Wettervorhersage verwenden.
Mikrosimulation
Die meisten Systeme bestehen aus mehreren Einzelbestandteilen.
In einer Mikrosimulation modellieren wir diese Einzelbestandteile und nicht das System als Ganzes. Bei einer Krankheitssimulation wird also das Verhalten der einzelnen Personen simuliert, bei einer chemischen Reaktion die Bewegung der einzelnen Gasatome
Für eine Mikrosimulation unserer Räuber-Beute-Beziehung modellieren wir Hasen und Luchse bzw. deren Verhalten als Individuen. Im Gegensatz zu einer Makrosimulation wird hier also jedes beteiligte Objekt individuell betrachtet und Populationsgrößen sowie andere Zustandsvariablen des Gesamtsystems durch die Simulation des Verhaltens und der Interaktion der individuellen Hasen und Luchse ersetzt.
3.2. Räuber-Beute-Simulation in Snap!

Schauen wir uns unsere Räuber-Beute-Simulation in Snap! an.
Öffnen Sie die Vorlage.
Klicken Sie auf die grüne Flagge, um die Simulation zu starten.
Beobachten Sie, was passiert!
Hinweise:
Grüne Flagge: Sie finden die grüne Flagge rechts oben in Snap!.
Eine mögliche Lösung finden Sie auf der nächsten Seite.
3.3. Räuber-Beute-Simulation in Snap! - Lösung I
Mögliche Lösung zum Vergleichen:
Hasen und Luchse laufen (zufällig) über den Bildschirm. Trifft ein Luchs auf einen Hasen, verschwindet der Hase. Luchse sterben nach einiger Zeit. Es entstehen allerdings kaum neue Hasen, sodass es schon nach einiger Zeit sehr wenige von ihnen gibt. Außerdem bewegen sich die Luchse sehr schnell.
3.4. Räuber-Beute-Simulation in Snap! - Mehr Hasen
Mehr Hasen zur Welt bringen
Aktuell werden kaum neue Hasen geboren. Erhöhen Sie die Wahrscheinlichkeit, sodass mehr neue Hasen entstehen!
Hinweise und Tipps:
Der klone-Block
Wenn wir unsere Simulation nun in Snap! entwerfen, dann benötigen wir für jeden Luchs und jeden Hasen ein Objekt (bzw. ein Sprite). Da wir nicht jeden Luchs bzw. Hasen einzeln modellieren wollen und können, nutzen wir das Prototypen-Konzept.
Was wir uns darunter vorstellen können, soll das untenstehende Beispiel verdeutlichen: Wenn wir an einen Barhocker denken, dann haben wir gewisse Vorstellungen wie ein solcher aussieht: Er hat einen langen Standfuß, eine runde Sitzfläche und ist gepolstert: Wir haben einen Prototyp vor Augen.
Allerdings sind auch andere Barhockerdesigns denkbar. Einen anderen Barhocker würden wir dann vielleicht so beschreiben: "Er sieht aus wie der erste Barhocker, ist aber rot." Wir passen unsere Beschreibung an, indem wir sagen, wie er sich vom Prototypen unterscheidet.
Genau wie wir im Beispiel mit den Barhockern einen (gedanklichen) Prototypen haben, erstellen wir für unsere Simulation je einen Prototypen für die Luchse und für die Hasen, legen deren Eingeschaften fest und spezifieren ihr Verhalten.
Sind wir damit zufrieden, klonen wir den Prototypen. Auch das machen wir natürlich nicht händisch, sondern mithilfe eines Blocks:

Tipp: Zwischen Hase und Luchs wechseln
Um zwischen Hasen- und Luchs-Prototypen zu wechseln, klicken Sie rechts unter der Bühne auf das passende Sprite (ProtoHase, ProtoLuchs).

In unserer Simulation wird ein Hase natürlich nicht geboren, er wird geklont. Können Sie die relevante Stelle im Code identifizieren?
Eine mögliche Lösung zum Vergleichen finden Sie auf der nächsten Seite.
3.5. Räuber-Beute-Simulation in Snap! - Lösung II
Mögliche Lösung (zum Vergleichen)
Eine mögliche Lösung ist es, im falls-Block anstelle der 1 eine 5 einzusetzen. Alternativ können Sie auch die 1000 durch eine kleinere Zahl ersetzen. Wir haben uns für Ersteres entschieden:

3.6. Räuber-Beute-Simulation in Snap! - Geschwindigkeit der Luchse reduzieren
Leider sind die Luchse deutlich zu schnell für unsere Simulation. Verringern Sie die Geschwindigkeit der Luchse!
Tipp: Die Bewegungsgeschwindigkeit der Luchse hängt mit dem Block gehe () Schritte zusammen.
Eine mögliche Lösung finden Sie auf der nächsten Seite.
3.7. Räuber-Beute-Simulation in Snap! - Lösung III
Mögliche Lösung:
Ändern Sie den Parameter in gehe(12) Schritte im Luchs-Sprite auf eine kleinere Zahl, z.B. 4.

3.8. Räuber-Beute-Simulation in Snap! - Erkenntnisse gewinnen
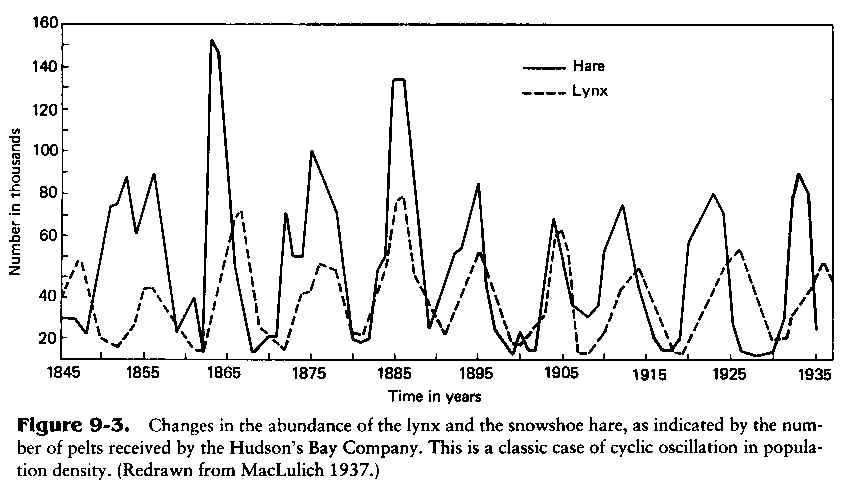
Durch Klick auf die Leertaste erhalten Sie ein Liniendiagramm, das Hasen (lila) und Luchse (gelb) gegenüberstellt. Beschreiben Sie Ihre Beobachtungen!
Mögliche Lösung zum Vergleichen:
Anhand der gejagten Felle hat die Hudson Bay Company die Populationen der Luchse bzw. Hasen für die Jahre 1845 bis 1937 erfasst.
Ein Blick auf die Grafik zeigt einen ähnlichen Verlauf wie in unserer Simulation! Das ist toll 🙂
Was wir damit entdeckt haben, ist die erste Lotka-Volterra-Regel:
"Erste Lotka-Volterra-Regel (Periodische Populationsschwankung): Die Populationsgrößen von Räuber und Beute schwanken periodisch. Dabei folgen die Schwankungen der Räuberpopulation phasenverzögert denen der Beutepopulation. Die Länge der Perioden hängt von den Anfangsbedingungen und von den Wachstumsraten der Populationen ab." (CC-BY-SA Wikipedia)
Sie können nun noch weitere Parameter manipulieren und den Effekt auf die Simulation untersuchen. Drücken Sie dann erneut die Leertaste, um einen Graphen der beiden Populationen zu erhalten.
Exkurs: Warum wir unseren eigenen berühre-Luchs-Block verwenden
Sie könnten auch einen der untenstehenden Blöcke verwenden:
![]()
![]()
Unsere Version ist aber deutlich schneller!
![]()
Dies hängt mit der internen Umsetzung zusammen: Unsere Version führt deutlich weniger Kollisionsabgleiche durch.
3.9. Simulation einer Pandemie
In Infizieristan ist ein besonders schweres Virus ausgebrochen. In dem Land leben 100 Menschen, von denen anfangs nur zwei Person infiziert sind. Mit Hilfe der Simulation soll es möglich sein, die folgende Frage zu beantworten:
Wie viel Prozent der Bevölkerung sollten zuhause bleiben, damit das Gesundheitssystem nicht überlastet wird?
Öffnen Sie dazu die Vorlage und modellieren Sie das Verhalten einer Person!
Lesen Sie dazu die Tipps aufmerksam durch!
In der Vorlage werden sie dazu das untenstehende Skript finden. Ihre Aufgabe ist es, das Verhalten einer Person zu modellieren.
Dazu unterscheiden wir drei Fälle (vgl. Kommentare im Skript):
- Im Falle, dass die Person nicht zuhause bleibt, sollte sie sich zufällig bewegen.
- Im Falle, dass die Person gesund ist und Kontakt zu einer kranken Person hat, sollten wir ihren Zustand auf krank ändern.
- Im Falle, dass die Person krank ist, sollten wir die Variable
erholungum 1 ändern. Hat die Variableerholungeinen Wert> 100erreicht, so sollten wir den Zustand der Person auf immun setzen.

Hinweis: mit Runde ist ein Durchlauf der fortlaufend-Wiederholung gemeint.
Sie merken, wir treffen dabei einige Annahmen:
- Personen, die nicht zuhause bleiben bewegen sich zufällig,
- bei Kontakt mit Kranken infizieren sich gesunde Personen sofort,
- nach 100 Zeiteinheiten werden kranke Personen immun.
Tipps:
Tipp: Simulation starten
Ein Klick auf die grüne Fahne rechts oben startet die Simulation, ein Klick auf das rote Stoppschild setzt sie zurück.
![]()
Um die Person zu bewegen, sind die folgenden Blöcke aus der Kategorie Bewegung hilfreich.



Damit das Verhalten weniger vorhersagbar wird, hilft dieser Block aus der Kategorie Operatoren.![]()
Wollen Sie wissen, ob die Person gerade eine kranke Person berührt, können Sie diesen Block aus der Kategorie Fühlen verwenden.
![]()
Die spitzen Klammern des Blocks weisen darauf hin, dass hier ein Wahrheitswert zurückgeliefert wird.
Welchen Block können wir dann verwenden, wenn wir etwas nur tun wollen, wenn eine bestimmte Bedingung erfüllt wird? Erinnern Sie sich?
Auflösung: Block für Bedingung
Tipp: Zustand ändern
Um den Zustand einer Person zu ändern, müssen wir die Variable zustand und ihr Kostüm ändern.


Mithilfe der Variable erholung können wir den Fortschritt im Genesungsprozess modellieren. Für unser Modell gehen wir davon aus, dass Personen zum Zeitpunkt der Infizierung eine erholung von 0 haben und sich diese jede Runde in der die Person krank bleibt um 1 erhöht.
Dazu können wir die Blöcke zum Setzen und Verändern von Variablen nutzen:


Dann müssen wir nur noch die Bedingung, ob der Wert größer als 100 ist, prüfen und den Zustand der Person entsprechend anpassen. Aber Sie wissen ja bereits, wie das geht.
Weitere Lösungshinweise, ein Nachmachvideo und eine mögliche Lösung zum Vergleichen finden Sie auf der nächsten Seite.
3.10. Simulation einer Pandemie - Lösung
Lösungshinweis: Genesung modellieren
Okay, wir helfen Ihnen 🙂

Nachmachvideo:
Mögliche Lösung zum Vergleichen:

Hier finden Sie das fertige Projekt.
4. Simulationen im Unterricht
Überblick über die Kapitel:
Simulationswerkzeuge für den Unterricht
Simulationen im Unterricht
4.1. Simulationswerkzeuge für den Unterricht
Auch wenn Sie am Ende des Moduls angekommen sind, ist an dieser Stelle natürlich noch längst nicht Schluss. Es gibt viele weitere Möglichkeiten und Ideen, wie Sie Simulationen für sich und für Ihren Unterricht verwenden können.
Im professionellen aber auch im Schulkontext gibt es eine Vielzahl von Simulationsprogrammen. Diese werden häufig jedoch nur sporadisch aktualisiert, manchmal ist das gewünschte Szenario gar nicht verfügbar oder die Installation der Software nicht möglich. Mit Werkzeugen wie Snap!, aber auch dem Emoji-Simulator, Netlogo oder sogar Tabellenkalkulationsprogrammen können wir auch selbst ganz leicht Simulationen erstellen.
Sammlung/ Beispiele:
Snap!:
Wie Sie Simulationen mit Snap! erstellen können, wissen Sie jetzt ja .
Mit der stärker verbreiteten Programmierumgebung Scratch funktioniert das ganz genauso.
Ideen für Simulationen in Scratch oder Snap! finden Sie übrigens in der ScratchCloud bzw. SnapCloud.

Eine sehr einfache Simulationsumgebung ist der Emoji-Simulator von Nicky Case. Dort können Sie beispielsweise die Simulation eines Waldbrandes, eines Räuber-Beute-Modells oder einer Epidemie ausprobieren. Oder Sie gestalten Ihr eigenes Modell und simulieren das.

NetLogo Web ist auf komplexere Simulationen ausgelegt. Zu den Beispielen auf der Website gehören die Simulation einer Ameisenkolonie oder einer DNA Proteinsynthese.
Um eine bestehendes Modell in NetLogo Web zu simulieren, klicken Sie zunächst auf Setup, dann auf Go.
Natürlich können Sie auch in NetLogo Web eigene Modelle erstellen

Tabellenkalkulationsprogramme bieten zwar weniger graphische Möglichkeiten, aber auch sie können für Simulationen (vor allem Makrosimulationen) verwendet werden. Beliebt bei der Simulation mit Tabellenkalkulationsprogrammen sind Simulationen von Zufallsexperimenten, aber auch eine Räuber-Beute-Simulation ist möglich.
Unsere Simulation mit Schneeschuhhasen und Luchsen könnten wir beispielsweise mithilfe eines Tabellenblattes realisieren. Dazu setzen wir auf eine rundenbasierte Neuberechnung der Populationszahlen. Wie das aussehen kann, finden Sie hier: Link.

4.2. Simulationen im Unterricht
Auch im Unterricht der verschiedensten Fächer bietet sich der Einsatz von Simulationen durchaus an. So ließe sich auch die Verbreitung von Informationen durch Personen und Bücher ähnlich wie die Simulation der Pandemie realisieren. Auch die Bevölkerungsentwicklung oder Veränderungen im Zugang zu Arbeit und Bildung durch höhere Mobilität von Menschen lassen sich simulieren. Damit sind Simulationen längst nicht nur für naturwissenschaftliche Fächer geeignet.
5. Selbsttest
6. Abschluss Modul 09
Super, Sie haben MODUL 09 erfolgreich beendet!

7. Literaturempfehlungen Modul 09


Verwendete Literatur im Überblick
- Lee, I. (2018): CT Webinars, URL
- Hartmann, W., & Hundertpfund, A. (2015): Digitale Kompetenz: Was die Schule dazu beitragen kann. hep verlag.
- Klügl, F. (2006). Multiagentensimulation. Informatik-Spektrum, 29(6), 412-415.
- Thomas, M. (2002): Informatische Modellbildung. Modellieren von Modellen als ein zentrales Element der Informatik für den allgemeinbildenden Schulunterricht. Potsdam, Diss.
- Nesbit, J., & Adesope, O. (2006): Learning with concept and knowledge maps: A meta-analysis. Review of educational research, 76(3), 413-448.
- Hunter, L. (2015): Wild Cats of the World. London: Bloomsbury Publishing. S. 146.
- Rothen, S. (1997): Wo Fuchs und Hase sich Gute Nacht sagen - Mit Excel ein Räuber-Beute-System simulieren. Luzern: M + K Computermarkt 97/12.
- Treiber, M., & Kesting, A. (2010). Verkehrsdynamik und-simulation: Daten, Modelle und Anwendungen der Verkehrsflussdynamik. Springer-Verlag.
- Vogel A. (2011): Einleitung. In: Der Buchmarkt als Kommunikationsraum. Wiesbaden: VS Verlag für Sozialwissenschaften.
- Jonassen, D. (2006): Modeling with technology: Mindtools for conceptual change. Upper Saddle River, NJ: Pearson Merrill Prentice Hall.