Beispiel: Aufstellen einer linearen Funktion (2 Punkte)
Abschlussbedingungen
Anzeigen
Beispiel
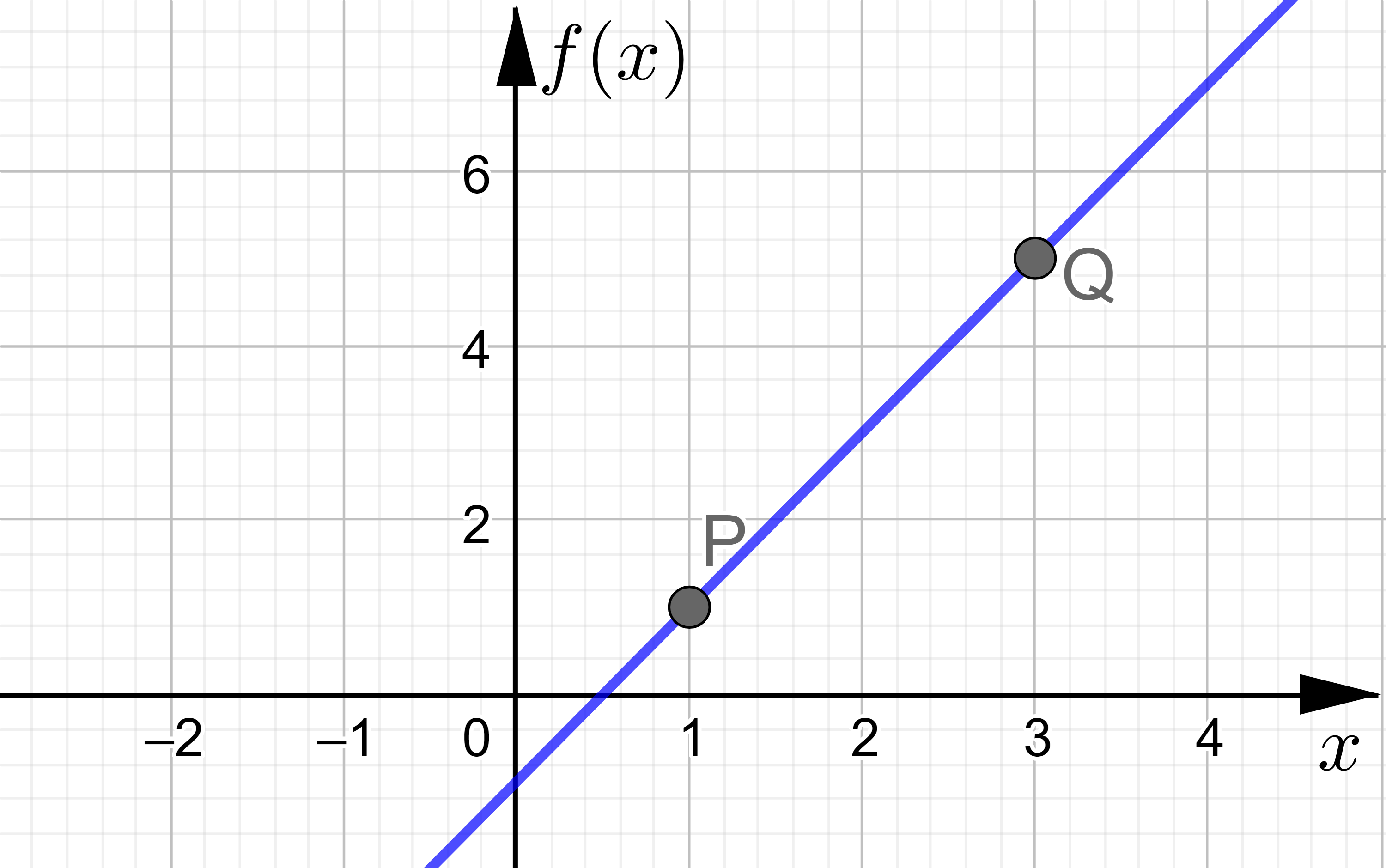
Die Punkte \(P(1|1)\) und \(Q(3|5)\) liegen auf dem Graphen der Funktion \(f(x)\).
Bestimmen Sie die Funktionsgleichung der Funktion.
Lösung
Mathematischer Ansatz
\(f(x)=m\cdot x + b \)
Steigung bestimmen
\(m=\dfrac{f(x_2) - f(x_1)}{x_2 - x_1} \)
\(m=\dfrac{5 - 1}{3 - 1} \)
\(m=\dfrac{4}{2} \)
\(m=2\)
Steigung einsetzen
\(m=2\)
\(f(x)=2\cdot x + b \)
Punkt einsetzen
Der Punkt \(P(1|1)\) hat allgemein die Einträge \(P(x|f(x))\)
Somit ist in diesem Beispiel \(x=1\) und \(f(x)=1\)
\(1=2\cdot 1 + b \)
umstellen
\(1=2\cdot 1 + b \)
\(1=2 + b \) \(|-2\)
\(-1= b \)
\(b= -1 \)
einsetzen
\(b=-1\)
\(f(x)=2\cdot x - 1 \)
oder
\(f(x)=2x - 1 \)
Zuletzt geändert: Montag, 8. März 2021, 20:52
