Info: Nullstelle einer linearen Funktion
Abschlussbedingungen
Anzeigen
Nullstelle (Lineare Funktion)
Erklärung
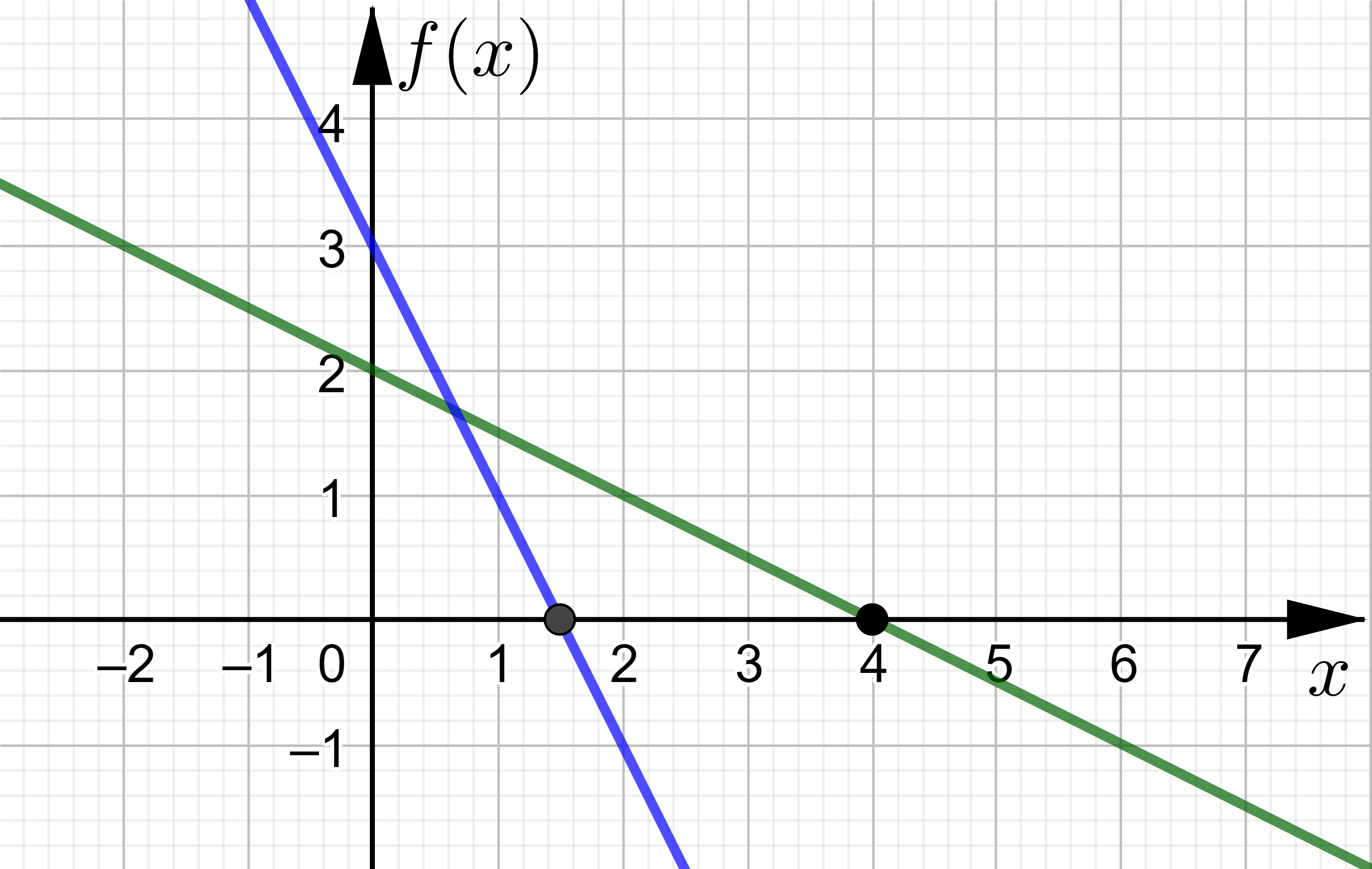
Die Stelle \(x\), an der der Funktionswert \(f(x)\) null wird (\(f(x)= 0 \)) und der Graph der Funktion die Abszisse (x-Achse) schneidet wird Nullstelle genannt.
Eine lineare Funktion mit der allgemeinen Form \(f(x)= m \cdot x + b \) besitzt genau eine Nullstelle.
Um die Nullstelle zu berechnen, muss die Gleichung \(0 = m \cdot x + b \) nach \(x\) umgestellt (gelöst) werden.
Mathematische Schreibweise
\(f(x)= m \cdot x + b \)
\(f(x)= 0 \)
\(0= m \cdot x + b \)
Zuletzt geändert: Mittwoch, 18. November 2020, 09:16
