Beispiel: Berechnen der Nullstelle einer linearen Funktionen
Abschlussbedingungen
Anzeigen
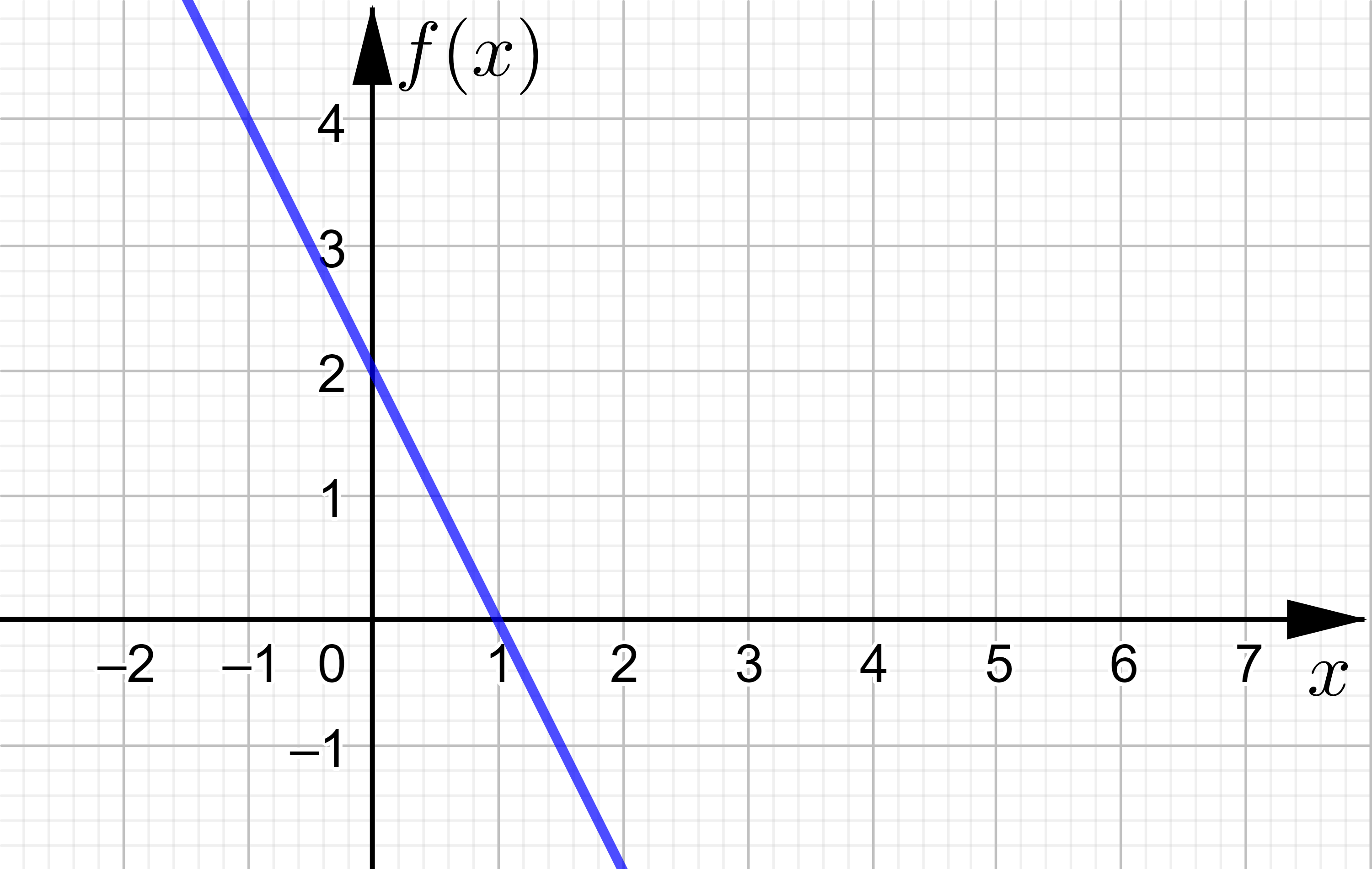
Bestimmen Sie die Nullstelle der Funktion \(f(x)=-2\cdot x + 2 \).
Mathematischer Ansatz
\(f(x)=0 \)
Ansatz einsetzen
\(f(x)=-2\cdot x + 2 \)
\(0=-2\cdot x + 2 \)
Gleichung umformen (lösen)
\(0=-2\cdot x + 2 \) \(|-2\)
\(-2=-2\cdot x\) \(|:(-2)\)
\(\dfrac{-2}{-2}=x\)
\(1=x\)
\(x=1\)
Die Funktion \(f(x)=-2\cdot x + 2 \) hat an der Stelle \(x=1\) eine Nullstelle.
Zuletzt geändert: Sonntag, 27. September 2020, 17:05
