Beispiel: Parameterdarstellung einer Geraden
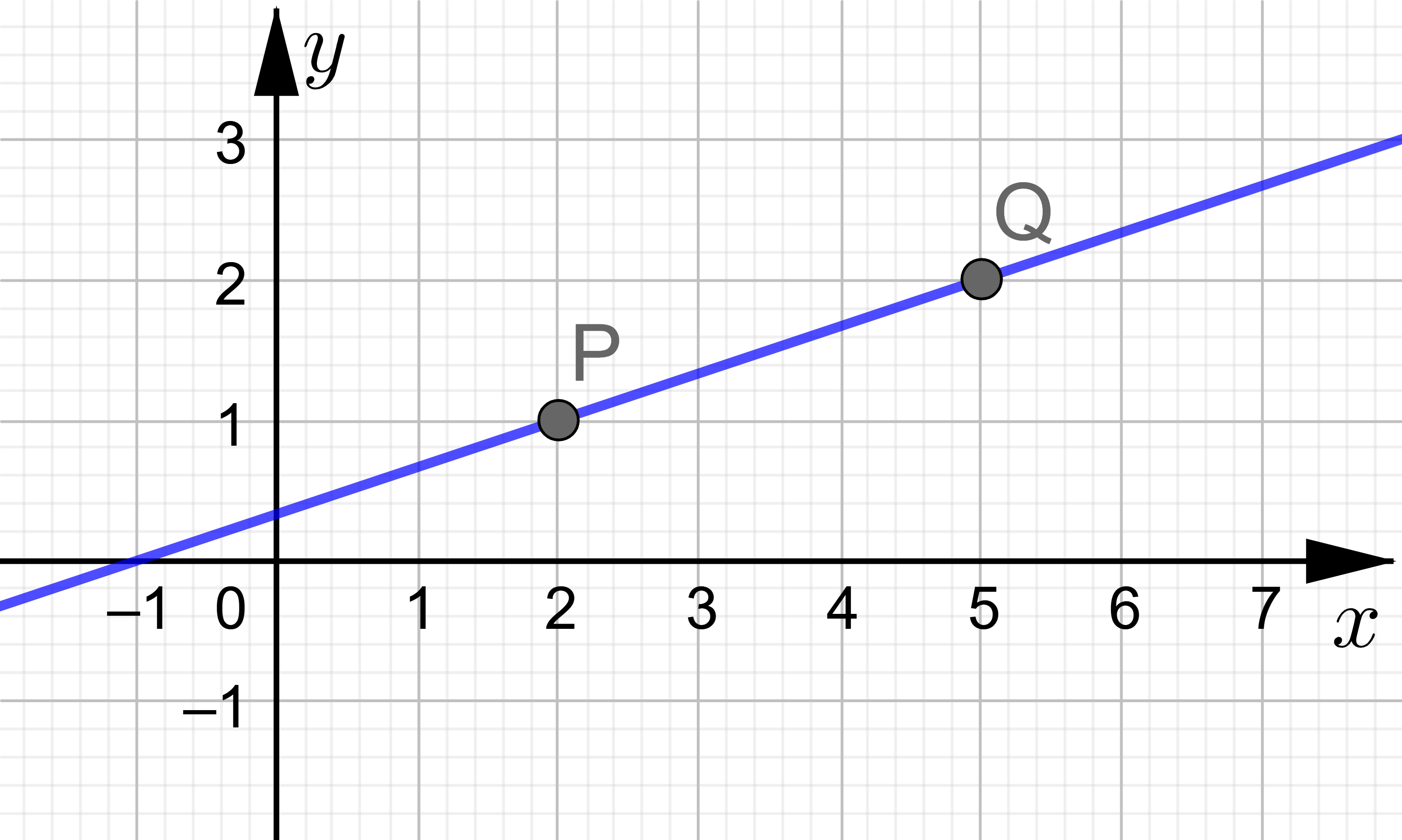
Bestimmen Sie für die Gerade \(g\) durch die Punkte \(P\) und \(Q\) die Geradengleichung in Parameterform.
\( g: \overrightarrow{x} = \overrightarrow{OP} + r \cdot \overrightarrow{PQ} \)
Ortsvektor zu Punkt \(P\) bestimmen.
\( \overrightarrow{OP} = \left(\begin{array}{c} 2 \\ 1 \end{array}\right) \)
Richtungsvektor von Punkt \(P\) zu Punkt \(Q\) bestimmen.
\( \overrightarrow{PQ} = \left(\begin{array}{c} 5 \\ 2 \end{array}\right) - \left(\begin{array}{c} 2 \\ 1 \end{array}\right) \)
\( \overrightarrow{PQ} = \left(\begin{array}{c} 5 - 2 \\ 2 - 1 \end{array}\right) \)
\( \overrightarrow{PQ} = \left(\begin{array}{c} 3 \\ 1 \end{array}\right) \)
Vektor in Geradengleichung einsetzen.
\( g: \overrightarrow{x} = \left(\begin{array}{c} 2 \\ 1 \end{array}\right) + r \cdot \left(\begin{array}{c} 3 \\ 1 \end{array}\right) \)
