Lösung: Mehrstufige Zufallsversuche
Bei einem Gewinnspiel, darf das Glücksrad zweimal gedreht werden.

a) Zeichnen Sie ein Baumdiagramm mit allen Variationen für den Ausgang des Glückspiels.
b) Berechnen Sie die Wahrscheinlichkeit für "Zweimal die gleiche Farbe".
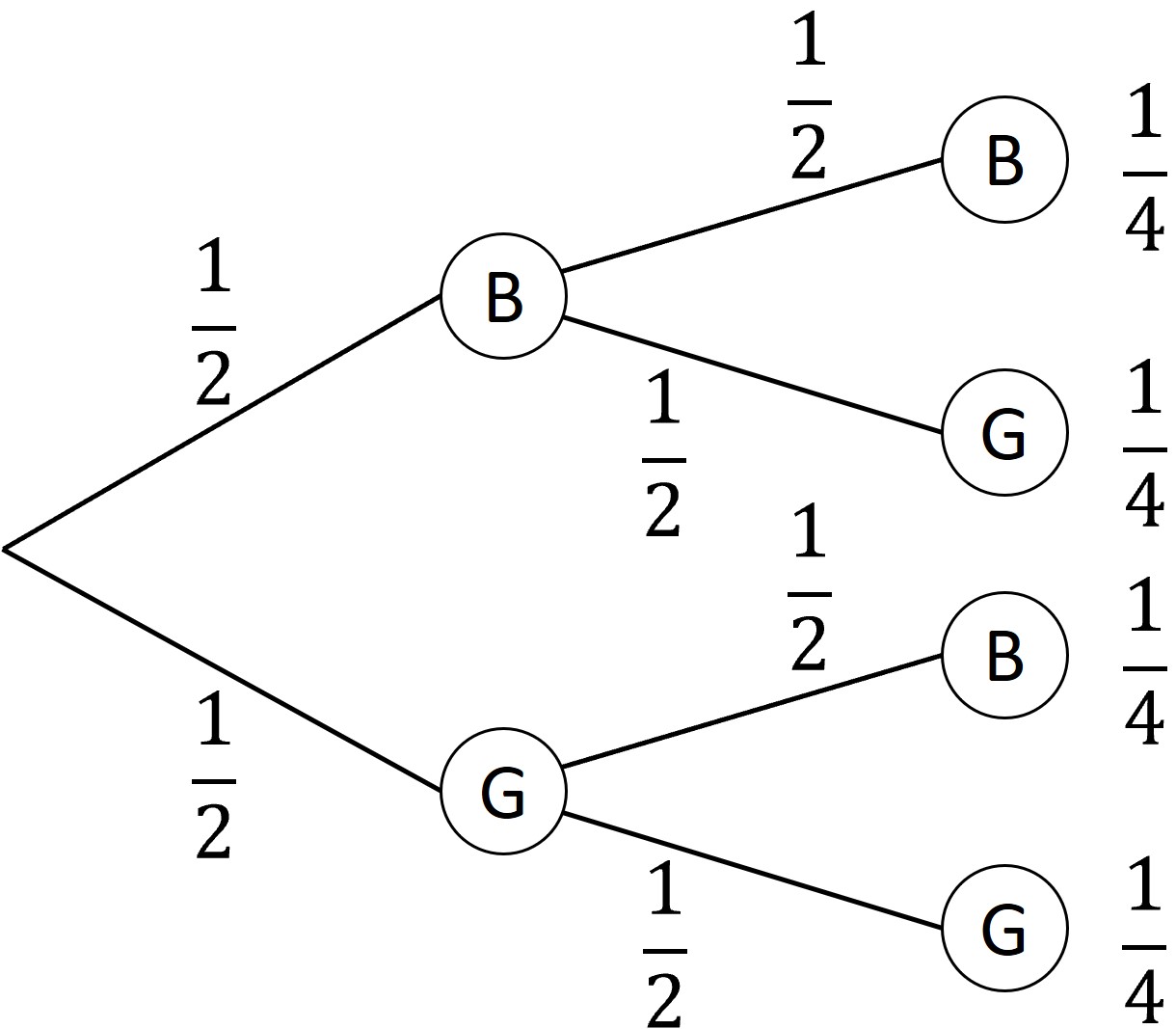
a) \(P(B)=\dfrac{1}{2}\)
\(P(G)=\dfrac{1}{2}\)
\(P(B \cap B)=P(B)\cdot P(B) \)
\(P(B \cap B)=\dfrac{1}{2}\cdot \dfrac{1}{2}=\dfrac{1}{4} \)
\(P(B \cap G)=P(B)\cdot P(G) \)
\(P(B \cap G)=\dfrac{1}{2}\cdot \dfrac{1}{2}=\dfrac{1}{4} \)
\(P(G \cap B)=P(G)\cdot P(B) \)
\(P(G \cap B)=\dfrac{1}{2}\cdot \dfrac{1}{2}=\dfrac{1}{4} \)
\(P(G \cap G)=P(G)\cdot P(G) \)
\(P(G \cap G)=\dfrac{1}{2}\cdot \dfrac{1}{2}=\dfrac{1}{4} \)
b) \(P(\text{"Gleiche Farbe"})=P(B \cap B)+P(G \cap G) \)
\(P(\text{"Gleiche Farbe"})=\dfrac{1}{4}+\dfrac{1}{4} \)
\(P(\text{"Gleiche Farbe"})=\dfrac{1}{2}\)
