Beispiel: Lineares Gleichungssystem aufstellen

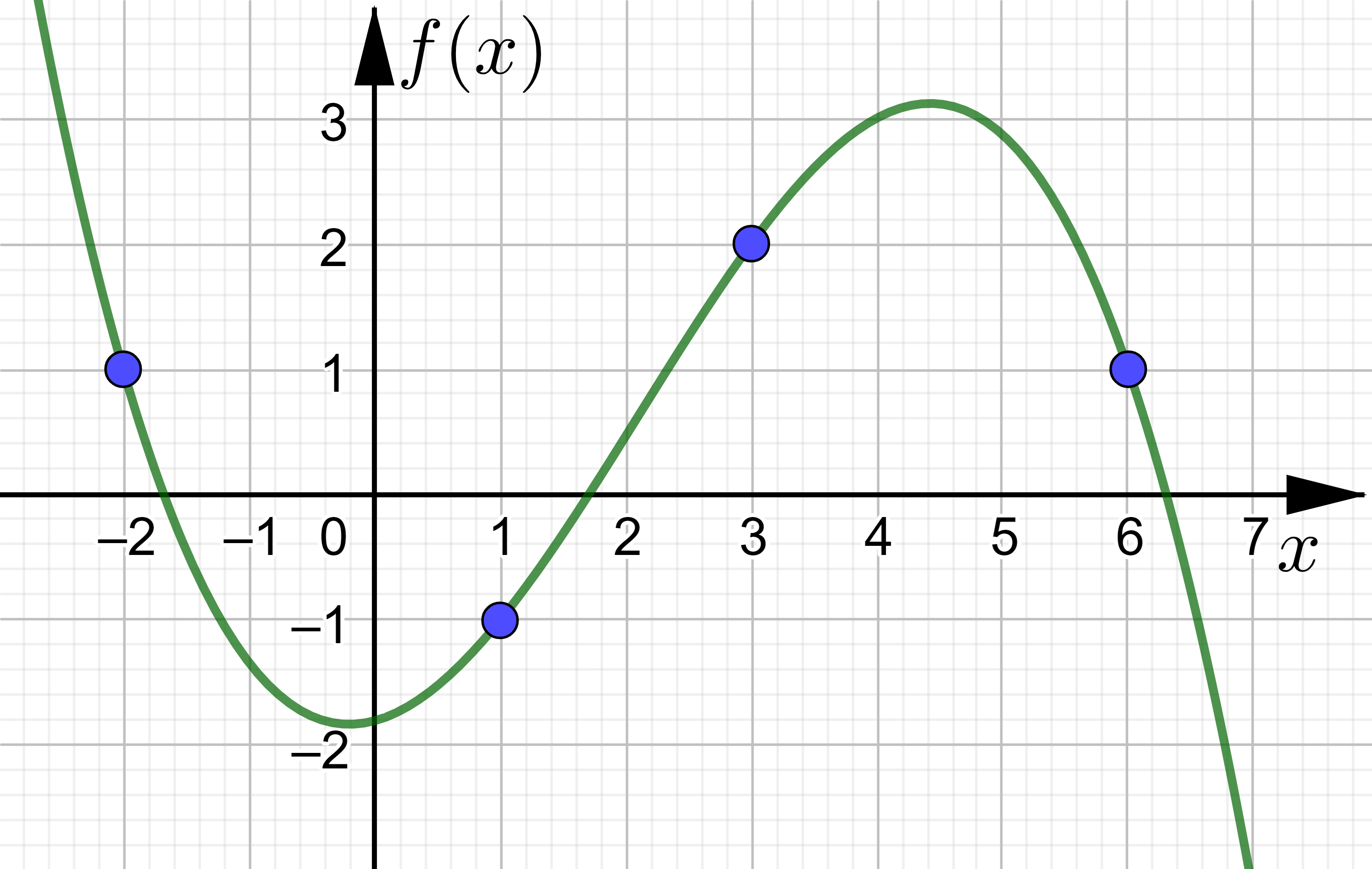
Zeigen Sie, dass der Graph der Funktion \(f(x)\) mit der Funktionsgleichung \( f(x)=-0,1 \cdot x^3 + 0,6333 \cdot x^2 + 0,2667 \cdot x -1,8 \) beschrieben werden kann.

Eigenschaften der Funktion

\( f(-2)=1 \)

\( f(1)=-1 \)

\( f(3)=2 \)

\( f(6)=1 \)

Allgemeine Form der Funktion

\( f(x)=a \cdot x^3 + b \cdot x^2 + c \cdot x + d \)

Eigenschaften (Bedingungen) in allgemeine Form einsetzen.

\( f(-2)=1 \) liefert: \( a \cdot (-2)^3 + b \cdot (-2)^2 + c \cdot (-2) + d = 1\)

\( f(1)=-1 \) liefert: \( a \cdot 1^3 + b \cdot 1^2 + c \cdot 1 + d = -1\)

\( f(3)=2 \) liefert: \( a \cdot 3^3 + b \cdot 3^2 + c \cdot 3 + d = 2\)

\( f(6)=1 \) liefert: \( a \cdot 6^3 + b \cdot 6^2 + c \cdot 6 + d = 1\)

Ausrechnen und als lineares Gleichungssystem schreiben.

\( \begin{matrix} I\\ II\\ III\\ IV \end{matrix} \begin{vmatrix} -8\cdot a & +4\cdot b & - 2\cdot c & + 1 \cdot d & = & 1 \\ 1\cdot a &+1\cdot b &+ 1 \cdot c & + 1 \cdot d & =& -1 \\ 27\cdot a &+ 9 \cdot b &+ 3\cdot c & + 1 \cdot d &=& 2 \\ 216\cdot a &+ 36 \cdot b &+ 6\cdot c & + 1 \cdot d &=& 1 \end{vmatrix} \)

Lineares Gleichungssystem lösen.

\( a=-0,1 \), \( b=0,6333 \), \( c=0,2667 \), \( d=-1,8 \),

Lösung in allgemeine Form der Funktion einsetzen.

\( f(x)=-0,1 \cdot x^3 + 0,6333 \cdot x^2 + 0,2667 \cdot x -1,8 \)