Beispiel: Flächeninhalt mit der Stammfunktion berechnen
Berechnen Sie den grün eingefärbten Flächeinhalt \(A\) der Funktion \(f(x)\).
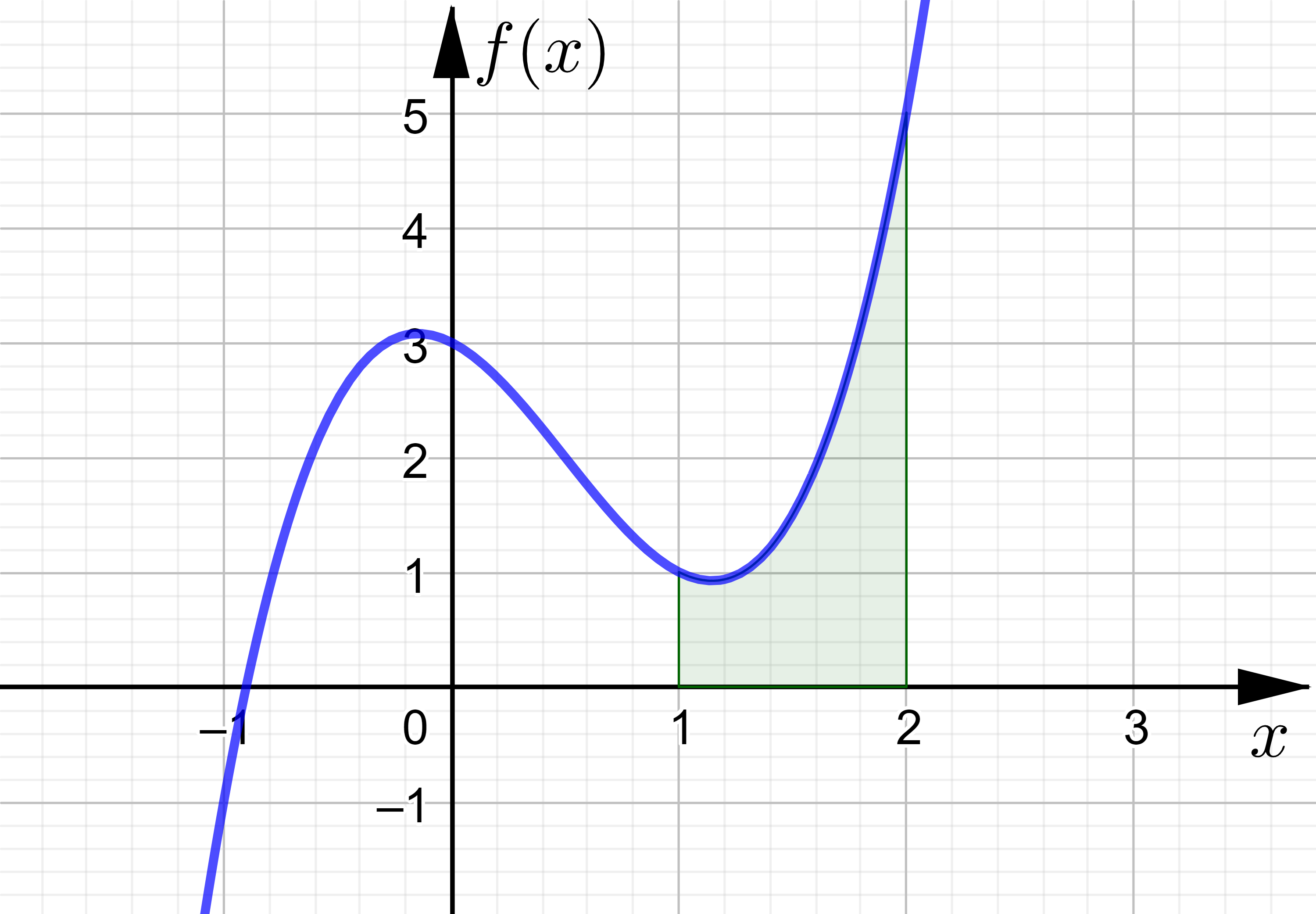
\(f(x)=2\cdot x^3-3\cdot x^2-x+3\)
Mathematischer Ansatz
\(A=\int \limits_{1}^{2} f(x)\,dx\)
Stammfunktion bilden
\(F(x)=\frac{1}{2}\cdot x^4-x^3-\frac{1}{2} \cdot x^2+3\cdot x+C\)
Flächeninhalt berechnen
\(A=\int \limits_{1}^{2} (2\cdot x^3-3\cdot x^2-x+3)\,dx=\Bigl[ \frac{1}{2}\cdot x^4-x^3-\frac{1}{2} \cdot x^2+3\cdot x+C \Bigr]_1^2\)
\(=\frac{1}{2}\cdot 2^4-2^3-\frac{1}{2} \cdot 2^2+3\cdot 2+C - \left(\frac{1}{2}\cdot 1^4-1^3-\frac{1}{2} \cdot 1^2+3\cdot 1+C\right)\)
Ab hier fällt die Konstante \(C\) weg, da \(C-C=0\)
\(=\frac{16}{2}-8-\frac{4}{2} +6 - \left(\frac{1}{2}-1-\frac{1}{2}+3\right)\)
\(=8-8-2 +6 - \left(\frac{1}{2}-1-\frac{1}{2}+3\right)\)
\(=4 - 2\)
\(=2\)
Der gesuchte Flächeninhalt von \(A\) ist \(2\) FE (Flächeneinheiten)
Hilfen zur Aufgabe:
