Lösungen: Extrempunkte, Hochpunkte und Tiefpunkte
Gegeben ist die folgende Funktion.
\(f(x)=-x^3+3x^2+9x-8\)
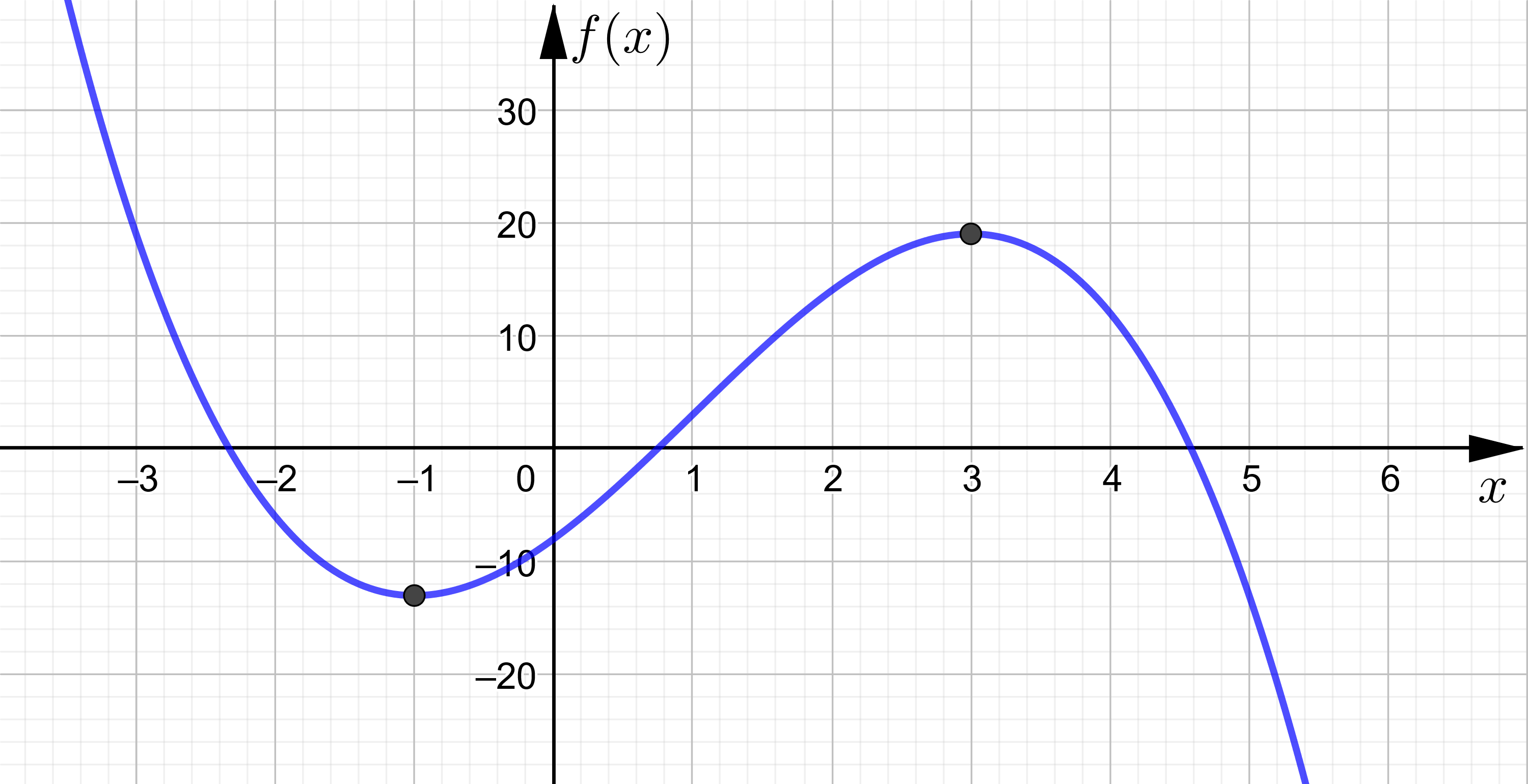
a) Bestimmen Sie die Stellen \(x_e\) der Funktion \(f(x)\) an den sich "möglicherweise" Extrempunkte befinden. (Notwendige Bedingung für Extremstellen)
\(f'(x_e)=0\)
\(f'(x)=-3x^2+6x+9\)
\(0=-3x^2+6x+9\)
Mit Taschenrechner lösen:
\(x_{e1}=-1\), \(x_{e2}=3\)
b) Weisen Sie mithilfe der 2. Ableitung nach, dass es sich tatsächlich im Extrempunkte handelt. (Hinreichende Bedingung für Extremstellen)
\(f''(x_e)\neq0\)
\(f''(x)=-6x+6\)
\(f''(-1)=12 \Rightarrow\) Extremstelle
\(f''(3)=-12 \Rightarrow\) Extremstelle
c) Untersuchen Sie, ob es sich bei den Extremstellen um einen Hochpunkt oder einen Tiefpunkt handelt.
Hochpunkt
\(f''(x_e)<0\)
\(f''(x)=-6x+6\)
\(f''(3)=-12 \Rightarrow\) Hochpunkt
Tiefpunkt
\(f''(x_e)>0\)
\(f''(x)=-6x+6\)
\(f''(-1)=12 \Rightarrow\) Tiefpunkt
d) Bestimmen Sie die Hochpunkte und Tiefpunkte
\(f(-1)=-13\)
\(T(-1|-13)\)
\(f(3)=19\)
\(H(3|19)\)
Hilfen zur Aufgabe:
Info: Bedingungen für Extremstellen
