Lösung: Berechnen der Nullstelle einer linearen Funktionen
Abschlussbedingungen
Anzeigen
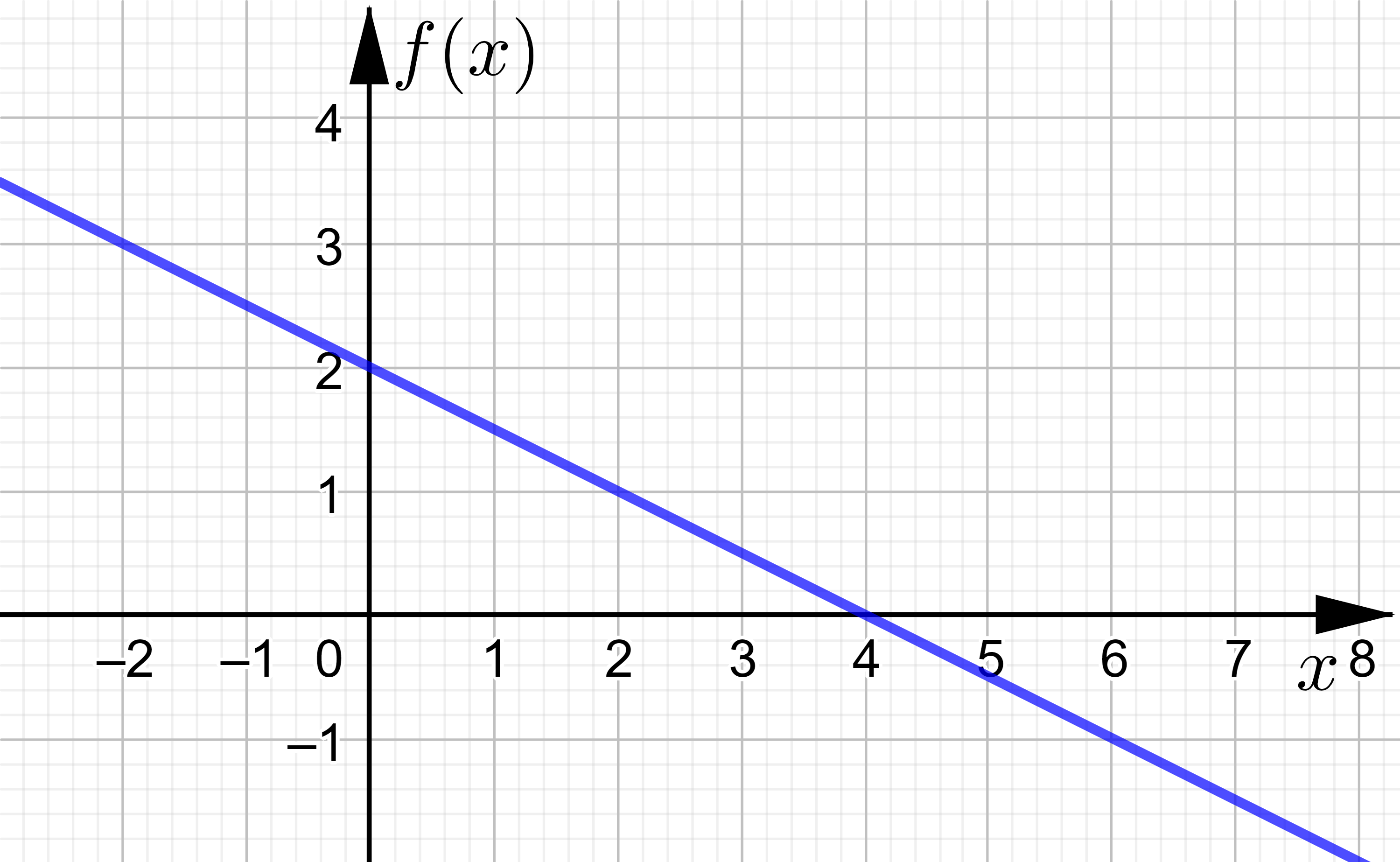
Berechnen Sie die Nullstelle der Funktion \(f(x)=-\dfrac{1}{2}\cdot x + 2 \).
Mathematischer Ansatz
\(f(x)=0 \)
Ansatz einsetzen
\(f(x)=-\dfrac{1}{2}\cdot x + 2 \)
\(0=-\dfrac{1}{2}\cdot x + 2 \)
Gleichung umformen (lösen)
\(0=-\dfrac{1}{2}\cdot x + 2 \) \(|-2\)
\(-2=-\dfrac{1}{2}\cdot x\) \(|:(-\dfrac{1}{2})\)
Rechenregel: Man teilt durch einen Bruch, indem man mit dem Kehrwert multipliziert ("mal nimmt").
\(-2\cdot-\dfrac{2}{1} =x\)
\(-2\cdot-2 =x\)
\(4=x\)
\(x=4\)
Die Funktion \(f(x)=-\dfrac{1}{2}\cdot x + 2 \) hat an der Stelle \(x=4\) eine Nullstelle.
Hilfen zur Aufgabe:
Info: Nullstelle einer linearen Funktion
Beispiel: Berechnen der Nullstelle einer linearen Funktionen
Zuletzt geändert: Sonntag, 27. September 2020, 17:28
